Fizyka.kopernik.mielec.pl - serwis fizyczny
 
• Mechanika »  Kinematyka, Dynamika, Praca, moc, energia, Grawitacja, Ruch obrotowy, Statyka, Relatywistyka • Fizyka molekularna i ciepło »  Termodynamika, Gazy, Ciecze, Ciała stałe • Elektryczność i magnetyzm »  Elektrostatyka, Pole elektrostatyczne, Prąd elektryczny stały, Magnetyzm, Elektromagnetyzm • Zjawiska falowe »  Ruch drgający i falowy, Akustyka, Drgania i fale elektromagnetyczne, Optyka • Elementy fizyki wpółczesnej »  Dualizm korpuskularno-falowy, Fizyka atomowa, Fizyka jądrowa • Astronomia »  Astronomia • Zagadnienia matematyczne »  Wektory, Pochodna funkcji, Logarytmy • Tablice »  Jednostki wielkości fizycznych, Właściwości fizyczne, Właściwości elektromagnetyczne i  falowe, Stałe fizyczne, Tablice matematyczne • O stronie »  Autorzy, Bibliografia
 Statyka
- Zjawisko równowagi
- Składanie sił
- Warunki równowagi
- Para sił
- Maszyny proste
- Środek ciężkości
- Rodzaje równowagi

Zjawisko równowagi

Równowagą nazywamy zjawisko, w którym działanie jednej siły jest równoważone przez działanie drugiej siły, ciała, na które działają te siły pozostaje w spoczynku. Dział mechaniki zajmujący się badaniem równowagi ciał nazywamy statyką. Dla uproszczenia opisu zjawisk w statyce pomija się odkształcenia ciała pod wpływem działania sił, wprowadzając pojęcie ciała sztywnego.

Ważną rolę w zjawisku równowagi odgrywają siły. Rozważmy dwa przypadki, w których działają siły wzajemnie się równoważące.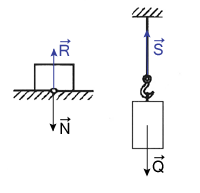

  1. leżący na podłożu klocek wywiera pod wpływem siły przyciągania nacisk prostopadły (normalny) N na podłoże, a równoważy tą siłę skierowana ku górze siła, zwana reakcją R, co powoduje, że klocek pozostaje w spoczynku
  2. ciężar Q bloku wiszącego nieruchomo na linie jest równoważony wywieraną przez linię i skierowaną wzdłuż niej siłą, zwaną naciągiem S


Jak już zostało w dziale dynamika stwierdzono siła jest wektorem, który charakteryzują następujące cechy: wielkość, kierunek działania, zwrot, punkt przyłożenia.

Wielkość siły jest to jej wartość liczbowa podawana zwykle w niutonach. Może być także wyrażona graficznie przez długość odcinka przedstawiającego wektor siły.

Kierunek działania siły określa się liczbowo przez podanie wartości kąta, jaki tworzy ona z pewnym kierunkiem umownym (najczęściej z kierunkiem poziomym ze zwrotem w prawo). Graficznie natomiast przedstawia się w postaci prostej odpowiednio skierowanej w płaszczyźnie rysunku, którą nazywamy linią działania.

Zwrot siły jest określany liczbowo wartością kąta, jaki tworzy ona z kierunkiem umownym albo graficznie strzałką na końcu wyobrażającego ja odcinka.

Punkt przyłożenia siły określa się liczbowo przez podanie jego współrzędnych w przyjętym układzie współrzędnych lub graficznie przez odpowiednie umiejscowienie na rysunku początku wyobrażającego ją odcinka ze strzałką.


Składanie sił
  • składanie sił przyłożonych w jednym punkcie i działających w jednej płaszczyźnie


    • Spróbujmy ustalić wypadkową pięciu sił przyłożonych w jednym punkcie i działających w jednej płaszczyźnie: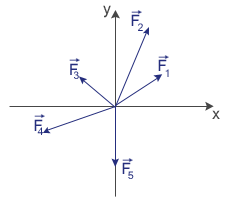



    Możemy to zrobić następująco: dodać pierwszą i drugą siłę i otrzymać ich wypadkową, następnie ta wypadkową składamy z trzecią siłą. Otrzymujemy wówczas wypadkową pierwszej, drugiej i trzeciej siły. Postępujemy analogicznie, otrzymujemy wypadkową czterech sił, a w końcu pięciu sił.



    Możemy jednak wykonać to zadanie w prostszy sposób, przy pomocy metody wieloboku. Mianowicie kreśląc z dowolnego punktu odcinek skierowany, wyobrażający pierwszą siłę, następnie z jego końca odcinek wyobrażający drugi odcinek, itd. Łącząc początek pierwszej siły z końcem ostatniej otrzymujemy siłę wypadkową.



    Wypadkowa układu sił przyłożonych w jednym punkcie i działających w jednej płaszczyźnie jest równa co do wielkości i kierunku bokowi zamykającemu wielobok zbudowany na odcinkach wyobrażających siły składowe.


  • składanie sił przyłożonych w różnych punktach i działających w jednej płaszczyźnie


    • Siłę działającą na ciało sztywne można przesunąć wzdłuż jej linii działania do innego punktu przyłożenia nie zmieniając przy tym skutku działania siły.


    Powyższa reguła pozwala nam na składanie sił przyłożonych w różnych punktach i działających w jednej płaszczyźnie, gdyż po przesunięciu sił, możemy je złożyć np. metodą równoległoboku.



    Trudniejszym natomiast do złożenia jest układ dwóch sił równoległych. Te siły nie można złożyć przez wyznaczenie przesunięcie ich i w ten sposób wyznaczyć wypadkową. Rozpatrzmy jednak układ dwóch sił równoległych i zgodnie skierowanych:



    Rysunek powyższy przedstawia sposób wyznaczenia wypadkowej dwóch sił równoległych. Zacznijmy jednak od początku. Siłę przesuwamy wzdłuż jej linii działania do punktu .Do sił i przykładamy siły: i . Następnie składamy odpowiednio siły, dzięki czemu otrzymujemy wypadkowe: i . Przesuwamy te wypadkowe według wcześniejszej reguły do punktu A. Takie wypadkowe możemy prosto złożyć metodą równoległoboku. Otrzymujemy wypadkową .



    Trójkąt jest podobny do trójkąta utworzonego przez siły: , a więc:



    Trójkąt jest podobny do trójkąta utworzonego przez siły: , a więc:



    Lewe strony obydwu równań są takie same, a więc możemy zapisać, że: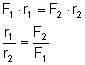



    Linia działania wypadkowej dwóch sił równoległych zgodnie skierowanych dzieli odległość między tymi siłami na odcinki odwrotnie proporcjonalne do ich wielkości.

    W podobny sposób możemy wyznaczyć wypadkową dwóch sił równoległych przeciwnie skierowanych. Jest ona równa różnicy tych sił i jest skierowana tak, jak siła o większej wartości liczbowej.

    Przekształcając podaną wyżej proporcję, otrzymujemy:



    W równaniu tym występują iloczyny będące momentami sił i . Możemy więc na podstawie naszych rozważań wysnuć wnioski:
    • suma momentów sił równoległych względem punktu leżącego na linii działania ich wypadkowej jest równa zeru
    • moment siły wypadkowej względem dowolnego punktu leżącego w płaszczyźnie układu jest równy sumie algebraicznej momentów sił składowych.



Warunki równowagi

Warunek równowagi sił przyłożonych w jednym punkcie i działających w jednej płaszczyźnie

Układ sił przyłożonych w jednym punkcie i działających w jednej płaszczyźnie jest w równowadze, jeżeli wielobok tych sił zamyka się sam przez się.


Oznacza to, że przy składaniu sił przyłożonych w jednym punkcie i działających w jednej płaszczyźnie metodą wieloboku sił, koniec ostatniej siły pokrywa się z początkiem siły pierwszej. Układ jest wtedy w równowadze.

Warunki równowagi sił dowolnie rozłożonych w płaszczyźnie:
  • wypadkowa wszystkich sił układu musi być równa zeru, co jest równoznaczne z warunkiem, aby wielobok tych sił zamykał się sam przez się
  • moment wypadkowy, tj. suma momentów wszystkich sił, względem dowolnego punktu w płaszczyźnie ich działania - musi być równa zeru, czyli:





Para sił

Istnieją takie układy sił, które mimo, iż nie mają wypadkowej, nie są siłami równoważącymi. Przykładem takiego układu, zwanego parą sił, są dwie siły równoległe, ale przeciwnie skierowane.

Obliczmy moment wypadkowy pary sił, złożonej z dwóch sił F (przeciwnie skierowanych), których linie działania są odległe o r. W tym celu należy wykonać sumę momentów tych sił względem dowolnego punktu O, odległego linii działania jednej z nich o x.



Suma momentów pary sił względem dowolnego punktu leżącego w płaszczyźnie ich działania jest jednakowa i równa iloczynowi jednej z sił i odległości r ich linii działania, zwanej ramieniem pary. Suma ta nosi nazwę momentu pary sił.



Maszyny proste

Maszynami prostymi nazywamy najprostsze narzędzia oraz części składowe mechanizmów, które służą do pokonywania dużych oporów za pomocą mniejszych sił o dogodnym kierunku ich działania.

Dźwignią nazywamy ciało sztywne osadzone obrotowo na osi lub podparte.



F - siła poruszająca
Q - opór użyteczny
R - reakcja osi

Dźwignie dzielą się na dwustronne (rysunek a i c) oraz na jednostronne (rysunek b). Dźwignie dwustronne mają środek obrotu lub punkt podparcia pomiędzy siłą poruszającą a oporem użytecznym, natomiast w dźwigniach jednostronnych punkty przyłożenia tych sił leżą po tej samej stronie osi obrotu.

f - ramię siły poruszającej
q - ramię oporu użytecznego

Ramię siły to odległość środka obrotu od linii działania, mierzone po prostopadłych.

Wykorzystując równanie momentów sił względem osi obrotu:



otrzymujemy zależność słuszną dla wszystkich odmian dźwigni: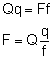



Krążek to okrągła tarcza, osadzona obrotowo na nieruchomej osi i zaopatrzona na obwodzie w rowek dla sznura, liny lub łańcucha. Krążek jest odmianą dźwigni.

Wyróżniamy dwa rodzaje krążków:
  • krążek stały - kierowniczy




    • Z równania momentów sił względem osi obrotu O, mamy:



    Opór użyteczny jest równoważony przez siłę poruszającą, a więc za pomocą tego rodzaju krążka możemy jedynie zmienić na bardziej dogodny kierunek działania siły poruszającej.

  • krążek przesuwny - ruchomy




    • Jeden koniec liny, na której wisi krążek, jest przytwierdzony nieruchomo, na drugi działa zaś siła poruszająca. Ciężar jest zawieszony na haku i działa na oś krążka. W miarę wyciągania liny krążek obraca się i podnosi jednocześnie. Korzystając z równania momentów sił względem osi obrotu O, mamy: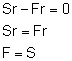



    Siła poruszająca jest równa sile naciągu. Z wieloboku sił otrzymujemy:



    Podstawiając wyżej obliczoną równość, mamy: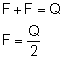



    A więc ten rodzaj krążka umożliwia dwukrotne zmniejszenie siły użytecznej w stosunku do oporu użytecznego. Najczęściej jednak używa się połączenia krążka stałego z krążkiem przesuwnym, przedstawionego na rysunku poniżej: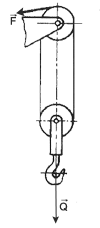



Kołowrotem nazywamy osadzony w łożyskach wał z umocowanym na nim kołem lub korbą.





Równią pochyłą nazywamy płaszczyznę lub tor prostoliniowy nachylony do poziomu pod określonym kątem.

Klin jest to graniastosłup trójkątny, którego dwie ściany boczne tworzą ze sobą niewielki kąt, zwany katem zbieżności, trzecia zaś stanowi grzbiet klina.

Śrubą nazywamy maszynę prostą w postaci walca, zaopatrzonego w występ biegnący wokół jego powierzchni w postaci linii śrubowej i jest wkręcana w nakrętkę zaopatrzoną w odpowiedni rowek śrubowy.



ZASADA ZACHOWANIA PRACY W MASZYNACH PROSTYCH

Praca wykonana przy pokonaniu oporu użytecznego za pomocą maszyny jest taka sama jak praca wykonana przy bezpośrednim pokonaniu go, bez użycia maszyny.



Środek ciężkości

Środek ciężkości to punkt, do którego jest przyłożona siła ciężkości. Środek ciężkości pokrywa się ze środkiem masy.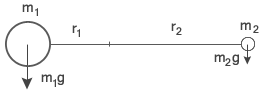





Środek masy to punkt, który spełnia warunek: .





Położenie środka ciężkości zależy od kształtu ciała i rozmieszczenia w nim cząstek. Dla ciał jednorodnych o kształtach określonych geometrycznych można go wyznaczyć na podstawie ich symetrii geometrycznych:
  • jeżeli ciało ma jedną oś symetrii, to środek ciężkości leży na tej samej osi
  • jeżeli ciało ma dwie lub więcej osi symetrii, to środek ciężkości leży na przecięciu się tych osi
  • jeżeli ciało ma środek symetrii, to punkt ten jest jednocześnie środkiem ciężkości.



Rodzaje równowagi

W zależności od położenia środka ciężkości wyróżniamy trzy rodzaje równowagi:
  • równowaga trwała - ma miejsce wtedy, gdy środek ciężkości jest położony w najniższym możliwym punkcie (wówczas energia potencjalna jest najmniejsza); przy odchyleniu ciała od położenia równowagi trwałej powstający moment ciężkości względem punktu podparcia lub zawieszenia powoduje jego powrót do położenia pierwotnego
  • równowaga chwiejna - ma miejsce wtedy, gdy środek ciężkości zajmuje najwyższe z możliwych położeń (energia potencjalna jest wówczas największa); przy odchyleniu od równowagi chwiejnej powstaje układ sił, który powoduje zmianę położenia do takiego, gdzie środek ciężkości zajmuje najniższe możliwe położenie i energia potencjalna jest najmniejsza
  • równowaga obojętna - ma miejsce wtedy, gdy linia działania siły ciężkości przechodzi niezależnie od położenia ciała przez punkt podparcia lub zawieszenia (energia potencjalna ma taką samą wartość we wszystkich położeniach); przy odchyleniu ciała względem położenia równowagi ciało pozostaje w miejscu, do którego zostało wychylone


Stopień trwałości równowagi ciał podpartych jest tym większy, im większe jest rozstawienie punktów podparcia oraz im niższe jest położenie środka ciężkości, bowiem potrzebna jest wtedy odpowiednio duża praca do wytrącenia ciała ze stanu równowagi i obrócenia wokół punktu podparcia.

fizyka.kopernik.mielec.pl - Statyka - wersja do wydruku Statyka - wersja do wydruku
Copyright © 2003-    fizyka.kopernik.mielec.pl