Fizyka.kopernik.mielec.pl - serwis fizyczny
 
• Mechanika »  Kinematyka, Dynamika, Praca, moc, energia, Grawitacja, Ruch obrotowy, Statyka, Relatywistyka • Fizyka molekularna i ciepło »  Termodynamika, Gazy, Ciecze, Ciała stałe • Elektryczność i magnetyzm »  Elektrostatyka, Pole elektrostatyczne, Prąd elektryczny stały, Magnetyzm, Elektromagnetyzm • Zjawiska falowe »  Ruch drgający i falowy, Akustyka, Drgania i fale elektromagnetyczne, Optyka • Elementy fizyki wpółczesnej »  Dualizm korpuskularno-falowy, Fizyka atomowa, Fizyka jądrowa • Astronomia »  Astronomia • Zagadnienia matematyczne »  Wektory, Pochodna funkcji, Logarytmy • Tablice »  Jednostki wielkości fizycznych, Właściwości fizyczne, Właściwości elektromagnetyczne i  falowe, Stałe fizyczne, Tablice matematyczne • O stronie »  Autorzy, Bibliografia
 Pochodna funkcji
- Pochodna funkcji w punkcie
- Różniczkowalność a ciągłość
- Interpretacja geometryczna pochodnej
- Interpretacja fizyczna pochodnej
- Pochodna jako funkcja
- Druga pochodna
- Twierdzenia o pochodnych
- Pochodne funkcji elementarnych

Pochodna funkcji w punkcie

Niech f oznacza funkcję zmiennej x, określoną w pewnym otoczeniu U punktu x0, zaś taką liczbę, że .

Iloraz



nazywamy ilorazem różnicowym funkcji f w punkcie x0 dla przyrostu h. Nazwa tego ilorazu pochodzi stąd, że w liczniku mamy różnicę wartości funkcji, zaś w mianowniku różnicę wartości argumentu, gdyż .

Jeżeli iloraz różnicowy ma granicę, gdy h dąży do zera, to tę granicę nazywamy pochodną funkcji f w punkcie x0 i oznaczamy f '(x0).


Mamy więc



Jeżeli granica istnieje to mówimy, że funkcja f ma pochodną w punkcie x0, lub że jest różniczkowalna w tym punkcie.


Różniczkowalność a ciągłość

Jeżeli funkcja f jest różniczkowalna w punkcie x0, to jest w tym punkcie ciągła.


Ciągłość funkcji jest warunkiem koniecznym dla istnienia pochodnej, choć nie jest warunkiem wystarczającym.


Interpretacja geometryczna pochodnej

Interpretacja geometryczna pochodnej przedstawiona jest na rysunku poniżej. Iloraz różnicowy jest równy tangensowi kąta nachylenia β siecznej AB do osi OX, czyli współczynnikowi kierunkowemu tej siecznej. Pochodna f'(x0), a więc granica ilorazu różnicowego jest równa współczynnikowi kierunkowemu stycznej do krzywej y=f(x) w punkcie A o odciętej x0: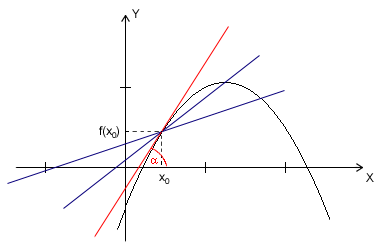

, gdzie α oznacza kąt nachylenia tej stycznej do osi OX.



Styczna do krzywej y = f(x) w punkcie P (x0, f(x0)) ma równanie




Interpretacja fizyczna pochodnej

Załóżmy, że punkt P porusza się po osi liczbowej OS i że współrzędna s punktu P jest funkcją czasu t.

Tę zależność s od t nazywamy równaniem ruchu. Jeżeli Δt oznacza przyrost czasu, to iloraz różnicowy



jest prędkością średnią punktu P od chwili t do chwili t + Δt. Granica tego ilorazu, gdy jest prędkością V(t) punktu P w chwili t:




Pochodna jako funkcja

Jeżeli funkcja f ma pochodną w każdym punkcie x pewnego przedziału (lub innego zbioru punktów), to określona jest w tym przedziale (zbiorze) funkcja zwana krótko pochodną funkcji f.


Druga pochodna

Jeżeli funkcja pochodna f ' jest różniczkowalna, to pochodną funkcji f ' nazywamy pochodną drugiego rzędu (drugą pochodną) funkcji f i oznaczamy symbolem f ''.


Twierdzenia o pochodnych

Jeżeli funkcje f i g mają pochodne w punkcie x, to:
  • , dla dowolnej stałej
  • , gdy
  • , gdy funkcja f ma pochodną w punkcie g(x), a funkcja g w punkcie x.

Pochodne funkcji elementarnych

Wzór funkcji Pochodna funkcji f Uwagi
 
 
x>0
 
 
dla
dla
a>0
 
x>0
a>0, , x>0
 
 


fizyka.kopernik.mielec.pl - Pochodna funkcji - wersja do wydruku Pochodna funkcji - wersja do wydruku
Copyright © 2003-    fizyka.kopernik.mielec.pl