
Definicja logarytmu
Niech a i b będą liczbami dodatnimi oraz
|
Wartość logarytmu może być dodatnia, ujemna lub równa zero. Z określenia logarytmu wynikają podane niżej własności:
gdzie:
Z definicji logarytmu wynikają natomiast następujące równości:
gdzie:
Logarytmem naturalnym nazywamy logarytm o podstawie e
Funkcja logarytmiczna
Niech
Sporządzimy teraz wykres funkcji logarytmicznej, korzystając z następującego twierdzenia:
|
Wykres funkcji
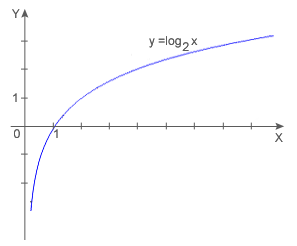
Wykres funkcji logarytmicznej nazywamy krzywą logarytmiczną. Krzywe logarytmiczne o równaniach
Własności funkcji logarytmicznej:
- Dziedziną funkcji jest zbiór liczb rzeczywistych dodatnich.

- Zbiorem wartości jest zbiór liczb rzeczywistych.

- Funkcja ma jedno miejsce zerowe: x=1.
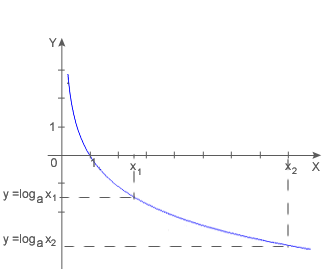
- Funkcja jest malejąca.
- Funkcja jest różnowartościowa.

- Dziedziną funkcji jest zbiór liczb rzeczywistych dodatnich.

- Zbiorem wartości jest zbiór liczb rzeczywistych.

- Funkcja ma jedno miejsce zerowe: x=1.
- Funkcja jest rosnąca.
- Funkcja jest różnowartościowa.
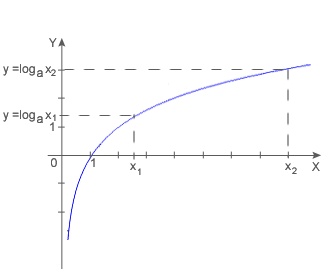
Własności logarytmów
- twierdzenie o logarytmie iloczynu
- twierdzenie o logarytmie ilorazu
- twierdzenie o logarytmie potęgi
- twierdzenie o zmianie podstawy logarytmu
Jeżeli a, x i y są liczbami dodatnimi oraz
|
Jeżeli a, x i y są liczbami dodatnimi oraz
|
Jeżeli a, x są liczbami dodatnimi oraz
|
Jeżeli a, b, x są liczbami dodatnimi oraz
Logarytmy dziesiętne
Logarytmy o podstawie 10 nazywamy logarytmami dziesiętnymi lub briggsowskimi - od nazwiska angielskiego matematyka Henry Briggsa, który w 1614 roku wprowadził je po raz pierwszy.
Zamiast
Logarytmy dziesiętne znalazły duże zastosowanie w obliczeniach astronomicznych i inżynierskich. Z tego powodu zostały ułożone tablice wartości tych logarytmów (patrz: tablice) i skonstruowano suwak logarytmiczny. Obecnie znaczenie logarytmów zmalało ze względu na wprowadzenie do powszechnego użytku kalkulatorów i innych urządzeń liczących.
Równania i nierówności logarytmiczne
|
|
Jak wiemy, wyrażenia logarytmowane i podstawa logarytmów muszą być dodatnie, przy czym podstawa logarytmu dodatkowo nie może być równa 1. Ograniczenia te wyznaczają dziedzinę równania lub nierówności logarytmicznej.
Jedną z metod rozwiązywania równań lub nierówności logarytmicznych jest doprowadzenie obu stron równania lub nierówności do logarytmy wyrażenia przy tej samej podstawie. Następnie wykorzystując różnowartościowość lub monotoniczność funkcji logarytmicznej o danej podstawie otrzymujemy związki między wyrażeniami logarytmowanymi. W najprostszych przypadkach możemy korzystać bezpośrednio z definicji logarytmu.
PRZYKŁADY:
- rozwiąż równanie
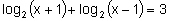 .
. - rozwiąż równanie
 .
. - rozwiąż równanie
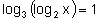 .
. - rozwiąż równanie
 .
. - rozwiąż nierówność
 , gdzie x>0.
, gdzie x>0. - rozwiąż nierówność
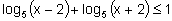 .
.
Zakładamy, że x+1>0 i x-1>0, czyli
Korzystamy ze wzoru na logarytm iloczynu:
Prawą stronę równania zapisujemy w postaci logarytmu:
Korzystamy z różnowartościowości funkcji logarytmicznej:

Rozwiązanie x=-3 jest sprzeczne z założeniem, a więc rozwiązaniem jest: x=3.
Zakładamy, że x>0. Podstawiamy

Wracamy do niewiadomej x i otrzymujemy:
Korzystamy z różnowartościowości funkcji logarytmicznej:
Zakładamy, że x>0 i
Dwukrotnie korzystamy z różnowartościowości funkcji logarytmicznej:

Logarytmujemy obie strony równania:
Korzystamy ze wzoru na logarytm potęgi:

Nie zmieniamy zwrotu nierówności, ponieważ funkcja
Zakładamy, że x-2>0 i x+2>0, czyli
Korzystamy z monotoniczności funkcji logarytmicznej:
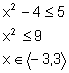
Po uwzględnieniu założenia, otrzymujemy: